Berekening van de buigkracht tijdens vrij buigen van plaatwerkbuigmachine

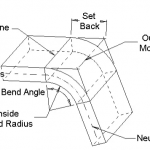
In de afgelopen jaren zijn buigmachines voor metalen remmen op grote schaal gebruikt in verschillende industrieën en het verwerkingsbereik van buigmachines is uitgebreid. Er is echter geen systematische discussie geweest over de berekening van de buigkracht. Momenteel worden er grofweg twee soorten buigkrachtberekeningsformules aanbevolen in de handleidingen van verschillende fabrikanten van kantpersbuigmachines.

P - buigkracht, KN;

S - plaatdikte, mm;

l - de buiglengte van het blad, m;

V - de breedte van de onderste matrijsopening, mm;

σb - Treksterkte van het materiaal, MPa.

De door de fabrikant aanbevolen buigkrachtparametertabel wordt ook berekend volgens de bovenstaande formule.

Het afleidingsproces en toepassingsbereik van de formule voor het berekenen van de buigkracht:

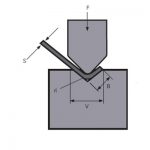
Figuur 1 is een schematisch diagram van het werk tijdens het buigen van platen. Het volgende beschrijft het afleidingsproces van de buigkrachtberekeningsformule en twee aanvullende parametervoorwaarden. Ten eerste zijn er dergelijke aanbevelingen in de producthandleiding. Bij vrijbuigen is de geselecteerde onderste matrijsopeningsbreedte V 8 tot 10 keer de plaatdikte S. Hier nemen we de aspectverhouding .

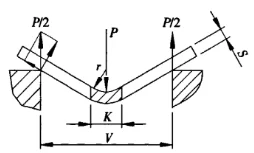
Figuur 1 Schematisch diagram van buigen

P - buigkracht

S - plaatdikte

V - onderste matrijsopeningsbreedte

r - de binnenradius wanneer de plaat is gebogen

K - de breedte van de horizontale projectie van de buigvervormingszone=9

Ten tweede vermeldt de fabrikant de overeenkomstige waarden van de matrijsbreedte V en de binnendiameter r van het buigwerkstuk op de buigkrachtparametertabel. Over het algemeen r=(0.16~0.17)V. Hier, de diameter-breedteverhouding: =0.16.

Tijdens het buigproces van het plaatwerk bevindt het materiaal in de vervormingszone zich in een zeer plastische vervormingstoestand en wordt het onder een hoek rond de middellijn gebogen. Op het buitenoppervlak van de buigzone kunnen in sommige gevallen microscheurtjes ontstaan. Op de dwarsdoorsnede van de vervormingszone, behalve in de buurt van de centrale laag, liggen de spanningen op andere punten dicht bij de treksterkte van het materiaal. Het bovenste deel van de neutrale laag wordt samengedrukt en het onderste deel wordt gespannen. Figuur 2 toont een doorsnede en bijbehorend spanningsdiagram in de vervormingszone.

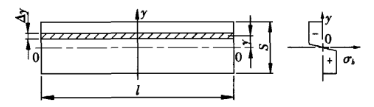
Figuur 2 Spanningsdiagram

S - plaatdikte

l - plaatbuiglengte

Het buigend moment op de doorsnede van de vervormingszone is:

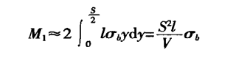
Het buigmoment dat wordt gegenereerd door de buigkracht van de machine in de vervormingszone is (zie figuur 1):

Van

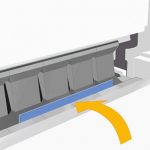
Bij het gebruik van universele mallen voor vrij buigen op een buigmachine, wordt het meeste plaatstaal 90° gebogen. Zoals weergegeven in figuur 3. K is:

Als we K in vergelijking (1) substitueren, krijgen we:

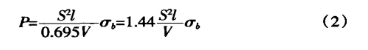
De treksterkte van gewone materialen σb=450N/mm2, waarbij formule (2) wordt vervangen door:

Uit het afleidingsproces blijkt dat wanneer vergelijking (2) of vergelijking (3) wordt gebruikt om de buigkracht te berekenen, de twee extra

Er moet aan de bovengenoemde parametervoorwaarden worden voldaan. Dat wil zeggen, de beeldverhouding= 9, de diameter-breedteverhouding=0.16, anders zal het een grote fout veroorzaken.

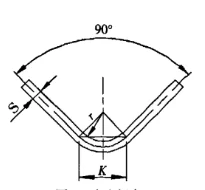
Figuur 3 Vrij buigen

S - plaatdikte

r - de binnenradius wanneer de plaat is gebogen

K - de breedte van de horizontale projectie van de buigvervormingszone

Nieuwe methoden en stappen voor het berekenen van de buigkracht

Door ontwerp- of proceseisen is het soms moeilijk om tegelijkertijd aan bovenstaande twee aanvullende eisen te voldoen. Op dit moment mag de aanbevolen berekeningsformule niet worden gebruikt om de buigkracht te berekenen, maar moet deze worden uitgevoerd volgens de volgende stappen.

(1) Volgens de plaatdikte S, de buigradius r en de onderste matrijsopening V, worden respectievelijk de breedte-dikteverhouding en de diameter-breedteverhouding berekend.

(2) Bereken de projectiebreedte van de vervormingszone volgens de vervorming van de plaat.

(3) Pas formule (1) toe om de buigkracht te berekenen.

Bij het berekeningsproces is rekening gehouden met het verschil van de buigradius en de verandering van de bijbehorende vervormingszone. De hieruit berekende buigkracht is nauwkeuriger en betrouwbaarder dan het resultaat dat wordt berekend met de gewoonlijk aanbevolen formule. Geef nu een voorbeeld ter illustratie, zoals weergegeven in figuur 4.

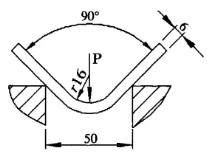
Figuur 4 Nieuwe rekenmethode

Bekend: De plaatdikte S=6mm, de plaatlengte l=4m, de buigradius r=16mm, de onderste matrijsopeningsbreedte V=50mm, en de materiaaltreksterkte σb=450N/mm2. Zoek de buigkracht die nodig is voor vrij buigen.

Zoek eerst de beeldverhouding en de verhouding tussen diameter en breedte:

Bereken vervolgens de projectiebreedte van de vervormingszone:

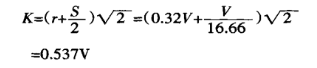
Gebruik tenslotte vergelijking (1) om de buigkracht te vinden:

Als de gebruikelijke aanbevolen formule wordt gebruikt om de buigkracht te berekenen:

Van = 1,5, is te zien dat het verschil tussen de twee 1,5 keer is. De reden voor deze fout is dat de buigradius in dit voorbeeld relatief groot is, en het corresponderende vervormingsgebied wordt vergroot, zodat er een grotere buigkracht nodig is tijdens het buigen. In dit voorbeeld is de diameter-breedteverhouding = 0,32, die de aanvullende voorwaarden van de hierboven geïntroduceerde parameters heeft overschreden. Het is uiteraard ongepast om de gewoonlijk aanbevolen formule te gebruiken om de buigkracht te berekenen. De voordelen van de nieuwe rekenmethode ziet u in dit voorbeeld.

Gevolgtrekking

De hier geïntroduceerde stappen en formules voor het berekenen van de buigkracht zijn niet alleen van toepassing op het hoekbuigen van plaatmetaal, maar ook van toepassing op het boogbuigen (strikt genomen zou het de hoekbuiging met een extra grote buigradius moeten worden genoemd). Opgemerkt moet worden dat de vorm van de mal bijzonder is wanneer de plaat in een boogvorm wordt gebogen. Bij het berekenen van de projectie van de vervormingszone, moet deze worden berekend volgens de technologische parameters die zijn ingesteld in het technologische proces, die niet kunnen worden uitgedrukt door een eenvoudige formule.

Bij het ontwerpen van een boogvormige mal kunnen bevredigende resultaten worden verkregen met behulp van de in dit artikel geïntroduceerde methode om de buigkracht te berekenen.